Stochastic Calculus Tutorial
More formally a map X. Tried to develop the theory of stochas-tic processes.

Statistics Stochastic Calculus With Ito S Lemma Part 1 Youtube
In this Wolfram Technology Conference presentation Oleksandr Pavlyk discusses Mathematicas support for stochastic calculus as well as the applications it e.

Stochastic calculus tutorial. Xt t Xt NU t tV2 t. DX t U tdt V tdW t where W t is a Brownian motion. This course is about stochastic calculus and some of its applications.
Stochastic calculus The mean square limit Examine the quantity E P n j1 Xt j Xt j 1 2 t 2 where t j jtn. In Chapter 2 we informally intro-duce the basic entities and operators of the Π Calculus and their appropriate representation in SpiFcpsyntax. You can see the high Stochastic shows us that price was very strong over the 5 candle period and that the recent candles are pushing higher.
An Ito di usion X t 0 tstochastic process described by a formal equation of the form. As the name suggests stochastic calculus provides a mathematical foundation for the treatment of equations that involve noise. That is at every timet in the set T a random numberXt is observed.
Or you might take a differential equation an equation relating a function to its derivatives and use it to figure out what the corresponding function looks like. Stochastic just means probability-related. Stochastic calculus is the area of mathematics that deals with processes containing a stochastic component and thus allows the modeling of random systems.
The transition matrix P is a stochastic matrix which is to say that pij 0 for all ij and P j pij 1 for all i. For stochastic differential equation. 12 Stochastic Processes Definition.
R B F RB where B are the Borel sets of the time space R. A low Stochastic number. T T wheret usually denotes time.
95 60 100 60 100 88. DW_tA standard Wiener process has a drift rate ie. Join Millions of Learners From Around The World Already Learning On Udemy.
Most of Chapter 2 is standard material and subject of virtually any course on probability theory. T T is a discrete-time process if the set T is finite or countable. We therefore say Xn j1 Xt j Xt j 1 2 t.
Where means has approximately the distribution. In normal calculus you might take a function and find its derivatives gradient curvature etc as time changes. Measurable Process The process X t.
Loosely speaking this means that for small increments. Many stochastic processes are based on functions which are continuous but nowhere differentiable. ConsequentlyifwecomputedYandkeepalltermsoforderdtordt12we obtain dYu dX 1 2 u dX2.
We can write the derivative of Wiener process over time t in this form. Ad Learn Calculus Online At Your Own Pace. Introduction to Stochastic Calculus - 11 IntroductionConditional ExpectationMartingalesBrownian motionStochastic integralIto formula For an event B and an random variable X the conditional.
Therefore we adhere closely to the concise Stochastic Π Calculus and only rarely add functionalities beyond its original core. Start Today and Become an Expert in Days. The tutorial is constructed as follows.
The various problems which we will be dealing with both mathematical and practical are perhaps best illustrated by consideringsome sim-. Offhandwewouldguessfrom3that dYu dXu bdtu dW accordingto the usual chain rule where d dx. Ad Learn Calculus Online At Your Own Pace.
As n 1this tends to zero. Because Xt j Xt j 1 is Normally distributed with mean zero and variance tn ie. A TUTORIAL INTRODUCTION TO STOCHASTIC ANALYSIS AND ITS APPLICATIONS by IOANNIS KARATZAS Department of Statistics Columbia University New York NY.
10027 September 1988 Synopsis We present in these lectures in an informal manner the very basic ideas and results of stochastic calculus including its chain rule the fundamental theorems on the represen-. What stochastic differentialequationdoes YtuXt t0 solve. Ito di usions are the main objects of study in stochastic calculus.
Also Chapters 3 and 4 is well covered by the litera-. Conversely a low Stochastic value indicates that the momentum to the downside is strong. In fact as we willsee 4 dWdt12 insomesense.
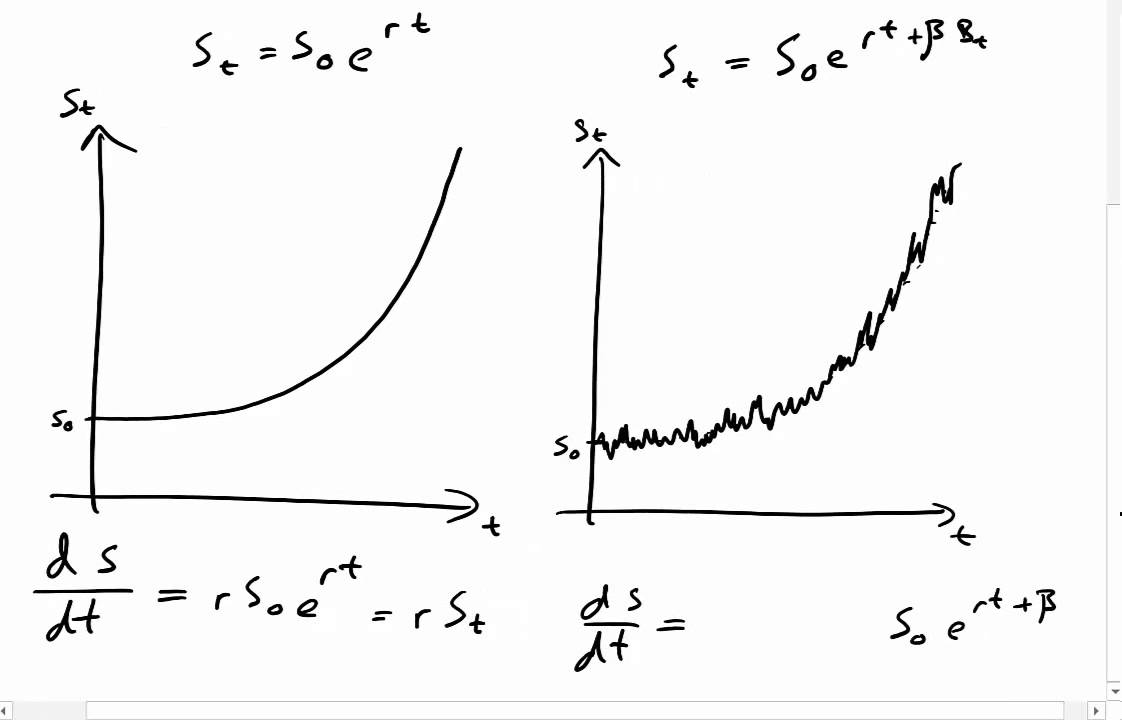
Stochastic calculus is a useful tool in financial maths. This rules out differential equations that require the use of derivative terms since they are unable to be defined on non-smooth functions. The binomial bnp distribution is a sum of nindependent Bernoullis bp.
Stochastic Process Given a probability space FP and a measurable state space EE a stochastic process is a family X t t 0 such that X t is an E valued random variable for each time t 0. Start Today and Become an Expert in Days. E Xt j Xt j 12 tn one can then easily show that the above expectation behaves like O1 n.
A stochastic process is a familyof random variables Xt. Average change per unit time of 0 and a variance rate of 1 per unit time. This is wrong however.
The value of the Stochastic indicator. Join Millions of Learners From Around The World Already Learning On Udemy. Therefore if we apply Corrolary 59 ntimes to the generating function q ps of the Bernoulli bp distribution we immediately get that the generating function of the binomial is q psq ps q psn.
In practice this generally means T 0123. The mean change per unit time for a stochastic process is known as the drift rate and the variance per unit time is known as the variance rate. 1Andrey Andreyevich Markov Russian mathematician 1856-1922.
Tucson or when incorporating probability in calculus courses at Caltech and Harvard University.

L21 3 Stochastic Processes Youtube

Jual Buku Cetak Stochastic Calculus For Quantitative Finance Kota Bogor Reading Books Tokopedia
Outline Of Stochastic Calculus Youtube
